Elliptische-Kurven-Kryptografie (ECC)
Was ist Elliptische-Kurven-Kryptografie (ECC, Elliptic Curve Cryptography)?
Die Kryptographie mit elliptischen Kurven (ECC) ist eine Verschlüsselungstechnik für öffentliche Schlüssel, die auf der Theorie der elliptischen Kurven beruht und mit der schnellere, kleinere und effizientere kryptographische Schlüssel erstellt werden können.
ECC ist eine Alternative zum kryptografischen Algorithmus Rivest-Shamir-Adleman (RSA) und wird am häufigsten für digitale Signaturen in Kryptowährungen wie Bitcoin und Ethereum sowie für die Einwegverschlüsselung von E-Mails, Daten und Software verwendet.
Eine elliptische Kurve ist keine Ellipse oder ovale Form, sondern wird als eine Schleifenlinie dargestellt, die zwei Achsen schneidet, die in einem Diagramm die Position eines Punktes angeben. Die Kurve ist vollständig symmetrisch oder gespiegelt entlang der x-Achse des Diagramms.
Kryptografiesysteme mit öffentlichem Schlüssel, wie ECC, verwenden einen mathematischen Prozess, um zwei verschiedene Schlüssel zusammenzuführen und dann die Ausgabe zum Ver- und Entschlüsseln von Daten zu verwenden. Der eine ist ein öffentlicher Schlüssel, der jedem bekannt ist, und der andere ist ein privater Schlüssel, der nur dem Absender und dem Empfänger der Daten bekannt ist.
ECC generiert Schlüssel durch die Eigenschaften einer elliptischen Kurvengleichung anstelle der traditionellen Methode der Generierung als Produkt großer Primzahlen. Aus kryptographischer Sicht können die Punkte entlang des Graphen mit der folgenden Gleichung formuliert werden:
y²=x³ + ax + b
ECC funktioniert wie die meisten anderen Verschlüsselungsmethoden mit öffentlichem Schlüssel, beispielsweise der RSA-Algorithmus und Diffie-Hellman. Jeder dieser Verschlüsselungsmechanismen verwendet das Konzept einer Einweg- oder Falltürfunktion. Das bedeutet, dass eine mathematische Gleichung mit einem öffentlichen und einem privaten Schlüssel verwendet werden kann, um einfach von A nach B zu gelangen. Ohne Kenntnis des privaten Schlüssels und abhängig von der verwendeten Schlüsselgröße ist es jedoch schwierig, wenn nicht gar unmöglich, von B nach A zu gelangen.
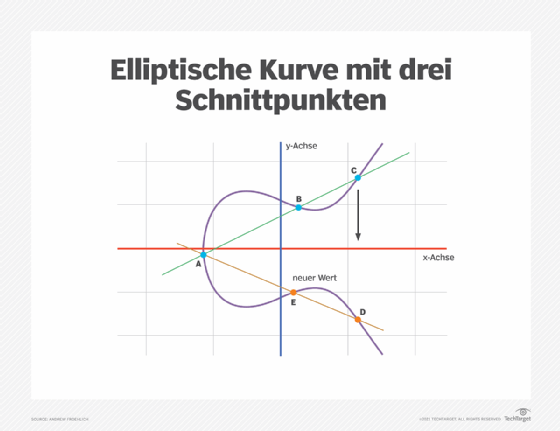
ECC basiert auf den Eigenschaften einer Gruppe von Werten, für die Operationen an zwei beliebigen Gliedern der Gruppe durchgeführt werden können, um ein drittes Glied zu erzeugen, das von den Punkten abgeleitet wird, an denen die Linie die Achsen schneidet, wie mit der grünen Linie und den drei blauen Punkten im untenstehenden Diagramm mit den Bezeichnungen A, B und C dargestellt. Die Multiplikation eines Punktes auf der Kurve mit einer Zahl ergibt einen weiteren Punkt auf der Kurve (C). Wenn man den Punkt C an den gespiegelten Punkt auf der gegenüberliegenden Seite der x-Achse bringt, erhält man den Punkt D. Von hier aus wird eine Linie zurück zu unserem ursprünglichen Punkt A gezogen, wodurch ein Schnittpunkt im Punkt E entsteht. Dieser Vorgang kann n-mal innerhalb eines bestimmten Maximalwerts durchgeführt werden. Das n ist der Wert des privaten Schlüssels, der angibt, wie oft die Gleichung durchlaufen werden soll, bis der endgültige Wert erreicht ist, der zur Ver- und Entschlüsselung von Daten verwendet wird. Der maximal definierte Wert der Gleichung bezieht sich auf die verwendete Schlüsselgröße.
Vergleich zwischen RSA und elliptischer Kurvenkryptografie
ECC kann ein Sicherheitsniveau bieten, das im Vergleich zu alternativen Methoden wie RSA weniger Rechenressourcen für die Ver- und Entschlüsselung von Daten erfordert. Beispielsweise würde ECC mit einem 256-Bit-Schlüssel einen 3.072-Bit-RSA-Schlüssel erfordern, um einen gleichwertigen Schutz zu erreichen. Da ECC eine gleichwertige Sicherheit bei geringerer Rechenleistung und geringerer Leistungsaufnahme als RSA erfordert, wird es häufig für mobile Anwendungen und Geräte des Internets der Dinge (IoT) mit begrenzten CPU-Ressourcen verwendet.
ECC bietet im Vergleich zu RSA mehrere Vorteile:
- Es funktioniert auf Geräten mit geringen CPU- und Speicherressourcen.
- Es verschlüsselt und entschlüsselt schneller.
- Größere Schlüssellängen können verwendet werden, ohne dass sich die Schlüsselgröße oder die CPU- und Speicheranforderungen wesentlich erhöhen.
Wie sicher ist die Kryptografie mit elliptischen Kurven?
ECC gilt als sehr sicher, wenn die verwendete Schlüssellänge groß genug ist. Die US-Regierung schreibt für die interne Kommunikation die Verwendung von ECC mit einer Schlüsselstärke von entweder 256 oder 384 Bit vor, je nach Sensibilitätsgrad der zu übertragenden Informationen.
ECC ist jedoch im Vergleich zu Alternativen wie RSA nicht unbedingt mehr oder weniger sicher. Der Hauptvorteil von ECC ist die inhärente Effizienz beim Verschlüsseln und Entschlüsseln von Daten.
Die Geschichte der Kryptographie mit elliptischen Kurven
Die Eigenschaften und Funktionen elliptischer Kurven in der Mathematik werden seit mehr als 150 Jahren untersucht. Ihre Verwendung in der Kryptografie wurde erstmals 1985 vorgeschlagen, und zwar von Neal Koblitz von der University of Washington und Victor Miller von IBM.
ECC wurde zunächst von Certicom, einem Anbieter von Sicherheitslösungen für den mobilen elektronischen Geschäftsverkehr, entwickelt und dann von Hifn, einem Hersteller von integrierten Schaltkreisen und Netzwerksicherheitsprodukten, lizenziert. Anbieter wie 3Com, Cylink Corp., Motorola, Pitney Bowes, Siemens, TRW Inc. (übernommen von Northrop Grumman) und Verifone unterstützten ECC in ihren Produkten.
Die Verwendung von ECC im öffentlichen und privaten Sektor hat in den letzten Jahren zugenommen. Zwar ist RSA nach wie vor weiter verbreitet und im Vergleich zu ECC einfacher zu verstehen, doch die Effizienzvorteile von ECC machen es für viele Anwendungsfälle in Unternehmen interessant. Dazu gehören die Beschleunigung des sicheren Zugriffs auf SSL-verschlüsselte Websites und das Streaming verschlüsselter Daten von IoT-Geräten mit begrenzter Rechenleistung.








