Perzeptron

Was ist ein Perzeptron?

Ein Perzeptron ist ein einfaches Modell einer biologischen Nervenzelle, das in künstlichen neuronalen Netzen (KNN) verwendet wird. Frank Rosenblatt stellte das Konzept 1957 vor, als er demonstrierte, wie es als Bestandteil eines einschichtigen neuronalen Netz eingesetzt werden kann. Das Perzeptron gilt als einer der frühesten Algorithmen, die für das überwachte Lernen von binären Klassifikatoren entwickelt wurden.

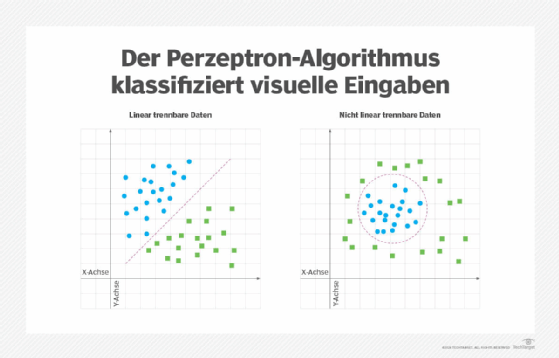
Der Perzeptron-Algorithmus wurde entwickelt, um visuelle Eingaben zu klassifizieren und sie in eine von zwei Kategorien zu gruppieren. Der Algorithmus geht davon aus, dass die Daten linear trennbar sind, das heißt dass sie auf natürliche Weise in zwei unterschiedliche Kategorien unterteilt werden können. Dieses Konzept lässt sich als zweidimensionale Ebene mit zwei Datensätzen visualisieren. Wenn diese Datensätze durch eine gerade Linie getrennt werden können, gelten sie als linear trennbar. Andernfalls sind sie nicht linear trennbar, wie in Abbildung 1 dargestellt.

Die Klassifizierung ist ein wichtiger Bestandteil des maschinellen Lernens und der Bildverarbeitung. Algorithmen für maschinelles Lernen verwenden verschiedene Methoden, um Muster in Datensätzen zu finden und zu kategorisieren. Eine dieser Methoden ist der Perzeptron-Algorithmus. Er führt eine binäre Klassifizierung durch, indem er die lineare Trennung zwischen den Datenpunkten findet, die über den Eingang des Perzeptrons empfangen werden.

Wie funktioniert das Perzeptron?

Das Perzeptron ist ein künstliches Neuron, das versucht, ein biologisches Neuron nachzubilden. Das Perzeptron nimmt eine oder mehrere gewichtete Eingaben entgegen und gibt eine einzige binäre Ausgabe zurück, entweder 1 oder 0. Abbildung 2 zeigt den Perzeptron-Algorithmus, wobei x der Eingabewert, w die Gewichtung der Eingabe und b der festgelegte Bias (Schwellenwert) ist.

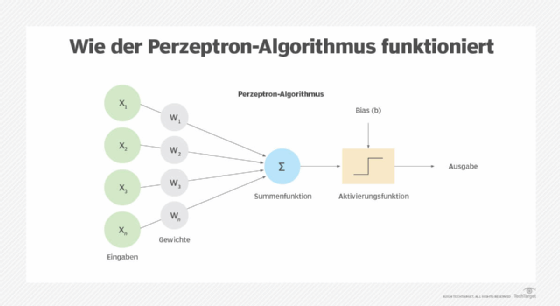
Der Perzeptron-Algorithmus kann auf verschiedene Weise dargestellt werden, oft unter Verwendung unterschiedlicher Namenskonventionen, aber die Grundkonzepte sind dieselben. Das Perzeptron besteht aus folgenden Komponenten:

• Eingaben. Das Perzeptron empfängt Daten von einer oder mehreren Eingabequellen. Jede Eingabe hat einen numerischen Wert, der ein Datenattribut darstellt.
• Gewichtung. Jeder Eingabewert wird eine numerisches Gewichtung zugewiesen. Die Gewichtung bestimmt die relative Stärke der Eingabe im Verhältnis zum Perzeptron als Ganzes. Der Eingabewert und die Gewichtung werden miteinander multipliziert, um einen gewichteten Wert für diese Eingabe zu erhalten.
• Summenfunktion. Die Funktion addiert die gewichteten Werte aller Eingaben. Aus diesem Grund wird die Summenfunktion manchmal auch als Nettoeingabefunktion bezeichnet.
• Bias (Schwellenwert). Dem Perzeptron wird ein bestimmter numerischer Wert zugewiesen, um die Ausgabe unabhängig von den Eingaben zu steuern, was zu einer größeren Flexibilität führt.
• Aktivierungsfunktion. Die Funktion führt eine Berechnung der Eingabesumme und Bias durch, um zu bestimmen, ob eine binäre 1 oder 0 zurückgegeben wird. Der genaue Ansatz hängt von der Art der Funktion ab. Für die Aktivierungsphase wird häufig eine Schrittfunktion verwendet, es gibt jedoch auch mehrere andere Arten von Aktivierungsfunktionen.
• Ausgabe. Das binäre Ergebnis der Aktivierungsfunktion.

Um besser zu verstehen, wie diese Komponenten zusammenwirken, betrachten Sie eine Situation, in der ein Entscheidungsträger anhand von vier Attributen entscheiden möchte, ob er ein Produkt kaufen soll. Jedes Attribut stellt eine binäre Eingabe in Form von wahr oder falsch (1 bzw. 0) dar. In Abbildung 3 sind die Attribute, ihre Eingabewerte und ihre Gewichte aufgeführt.

In diesem Szenario wird dem Attribut Garantie (das dritte in Abbildung 3) die größte Gewichtung und dem Attribut Angebot (das letzte) die geringste Gewichtung zugewiesen. Es überrascht nicht, dass die Art und Weise, wie die Eingaben gewichtet werden, einen großen Einfluss auf das Ergebnis haben kann. Die Summenfunktion addiert die gewichteten Eingaben mit dieser Formel:

z = x1w1 + x2w2 + x3w3 + x4w4

Die Summenfunktion gibt einen einzelnen Wert zurück, der dann von der Aktivierungsfunktion verwendet wird. Um die Eingabesumme für die Attribute zu bestimmen, können ihre Eingabewerte und Gewichtungen in eine Formel eingesetzt werden:

z = x1w1 + x2w2 + x3w3 + x4w4

z = (1 x 0,7) + (0 x 0,6) + (1 x 0,8) + (1 x 0,3)

z = 0,7 + 0 + 0,8 + 0,3

z = 1,8

Hier gibt die Summenfunktion (z) einen Wert von 1,8 zurück. Dieser Wert kann zusammen mit der Bias (b), der in diesem Fall den Wert 2 hat, in der Aktivierungsfunktion (a) verwendet werden. Aktivierungsfunktionen verwenden eine andere Logik zur Berechnung des binären Ausgabewerts. In diesem Beispiel wird die folgende Logik auf Summe und Bias angewendet:

a = 1, if z > b, else 0

Die Formel besagt, dass die Summe der Eingaben größer als der Bias sein muss, damit die Funktion den Wert 1 zurückgibt. Andernfalls gibt sie eine 0 zurück. Sie können diese Formel auf das obige Beispiel anwenden:

a = 1, if z > b, else 0

a = 1, if 1,8 > 2, else 0

a = 0

Die Eingangssumme überschreitet den Schwellenwert nicht, sodass das Perzeptron den Wert 0 zurückgibt. Dieses einfache Beispiel veranschaulicht die grundlegenden Konzepte der Funktionsweise des Perzeptrons und wendet eine einfache Logik an.

Ein Perzeptron kann auch über einen Lernalgorithmus trainiert werden. Während der Trainingsphase durchläuft das Perzeptron eine Phase des überwachten Lernens, bei der bereits bekannte Daten mit Kategorien verwendet werden. Basierend auf den Ergebnissen dieses Prozesses werden Gewichtungen und Bias des Perzeptrons angepasst, um dessen Genauigkeit zu verbessern.

Eine kurze Geschichte des Perzeptrons

Die Idee der künstlichen Neuronen geht auf Rosenblatts Arbeit zurück. Im Jahr 1943 veröffentlichten der Neurophysiologe Warren McCulloch und der Logiker Walter Pitts eine bahnbrechende Arbeit mit dem Titel A logical calculus of the ideas immanent in nervous activity (PDF), die das erste mathematische Modell eines neuronalen Netzwerks liefert. Ihr künstliches Neuron – das sogenannte McCulloch-Pitts-Neuron (MCP-Neuron) – empfängt binäre Eingaben und gibt eine binäre Ausgabe aus.

Bei der Entwicklung des Perzeptrons baute Rosenblatt auf den Konzepten des MCP-Neurons auf, verbesserte das Modell jedoch, um seine Flexibilität zu erhöhen. Er arbeitete 1957 am Cornell Aeronautical Laboratory an dem Perzeptron, wo er vom United States Office of Naval Research finanziell unterstützt wurde. Rosenblatt führte den Algorithmus zunächst auf einem IBM 704-Computer aus, der fünf Tonnen wog und einen ganzen Raum füllte. Das Projekt war der erste Schritt in Richtung einer maschinellen Umsetzung der Bilderkennung.

Im folgenden Jahr bauten Rosenblatt und seine Kollegen ihre eigene Maschine: das Mark I Perceptron. Der Computer enthielt eine Anordnung von 400 Fotozellen, die mit Perzeptronen verbunden waren. Die Gewichtung der Perzeptrone wurden in Potentiometern aufgezeichnet, die durch Elektromotoren eingestellt wurden. Das Mark I Perceptron war eines der ersten künstlichen neuronalen Netze, die jemals geschaffen wurden. Es befindet sich heute im National Museum of American History, das zum Smithsonian Institute gehört.

Als das Perzeptron vorgestellt wurde, glaubten viele, dass es einen bedeutenden Meilenstein auf dem Weg zur KI darstellte. Die technischen Grenzen des Perzeptrons wurden jedoch schnell deutlich, da einschichtige Perzeptrone Daten nur gruppieren können, wenn sie linear trennbar sind. Später entdeckten Datenwissenschaftler, dass sie mit mehrschichtigen Perzeptronen nicht linear trennbare Daten klassifizieren und damit Probleme lösen konnten, die mit einschichtige Algorithmen nicht zu bewältigen waren.