Hexadezimal-Zahlensystem
Was ist das Hexadezimal-Zahlensystem?
Hexadezimal ist ein Zahlensystem, das für numerische Werte eine Darstellung zur Basis 16 verwendet. Es lässt sich zur Darstellung großer Zahlen mit weniger Stellen nutzen. Das System hat 16 Symbole oder mögliche numerische Werte von 0 bis 9, gefolgt von sechs alphabetischen Zeichen: A (10), B (11), C (12), D (13), E (14) und F (15). Diese Zeichen stellen die Dezimalwerte 10 bis 15 in einzelnen Bits dar. In vielen Programmiersprachen wird bei Hexadezimalzahlen nicht zwischen Groß- und Kleinschreibung unterschieden (zum Beipiel FF oder ff).
Hexadezimal (Basis 16, kurz Hex) ist eines der wichtigsten Zahlensysteme in der Informatik, neben Dezimal (Basis 10), Binär (Basis 2) und Oktal (Basis 8).
Das Hexadezimalsystem verwendet andere Zahlen als das Dezimalsystem. Im Hexadezimalsystem werden 16 aufeinanderfolgende Zahlen, einschließlich 0, als Grundeinheiten verwendet. Die ersten neun Ziffern, 0 bis 9, sind die gleichen wie im Dezimalsystem. Die nächsten sechs zweistelligen Zahlen, 10 bis 15, werden durch die Buchstaben A bis F dargestellt. Das Hexadezimalsystem verwendet also die Ziffern 0 bis 9 und die Großbuchstaben A bis F, um die entsprechende Dezimalzahl anzugeben.
In diesem Zahlensystem ist jede Ziffer sechszehnmal wichtiger als die Ziffer an der vorherigen Position. Die Hexadezimalzahl beginnt mit der niedrigstwertigen Stelle rechts. Der numerische Wert dieser Zahl wird berechnet, indem jede Ziffer mit dem Wert ihrer Position multipliziert und die Produkte dann addiert werden. Aus diesem Grund ist Hexadezimal ein Stellenwertsystem oder ein gewichtetes Zahlensystem.

Warum sind Hexadezimalzahlen notwdenig?
In Computersystemen können die binären Entsprechungen großer Dezimalzahlen sehr lang werden. Wenn es sich um 16- oder 32-Bit-Zahlen handelt, wird es schwierig, sie fehlerfrei zu lesen und zu schreiben. Diese Probleme lassen sich lösen, indem man die Binärzahlen in Gruppen von vier Bits anordnet und dabei das hexadezimale Zahlensystem verwendet.
Das Format der Hexadezimalzahlen ist kompakter als das der Binärzahlen, da sie große Binärzahlen mit weniger Ziffern darstellen können. Sie sind daher leichter zu verstehen als lange binäre Zeichenketten aus Einsen und Nullen.
Programmierer verwenden Hexadezimalzahlen, weil ihre Zahlenwerte wesentlich kürzer sind als bei der Darstellung im Dezimalformat. Aus diesem Grund werden viele Computerfehlercodes und Speicheradressen im Hexadezimalformat dargestellt. Das Verständnis dieser hexadezimalen numerischen Ausdrücke ist für das Debuggen von Computersoftware daher unerlässlich. Hexadezimale numerische Ausdrücke finden sich auch in den Stoppcodes des Blue Screen of Death von Windows und in den HTML-Farbcodes (Hypertext Markup Language).
Darstellung von Hexadezimalzahlen
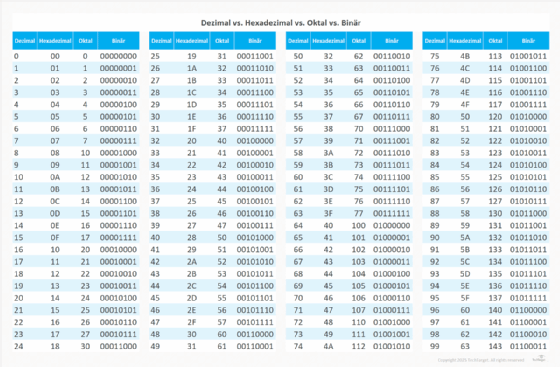
Eine einzige Hexadezimalziffer kann vier Ziffern einer Binärzahl darstellen. Durch die Unterteilung einer Binärzahl in 4-Bit-Gruppen (Nibble) kann jede Gruppe einen möglichen Wert zwischen 0000 und 1111 haben, was 16 Zahlenkombinationen von 0 bis 15 ermöglicht. Binäre Zahlen lassen sich leicht in hexadezimale Zahlen umwandeln und umgekehrt. Abbildung 3 zeigt, wie diese Zahlen in den beiden Systemen dargestellt werden:

Zusätzlich stellen die Ziffern links vom Dezimalpunkt einen Wert dar, der durch Potenzieren von Basis 16 mit der entsprechenden Zahl berechnet wird. Dies ergibt die Gewichte 160, 161, 162 usw. In ähnlicher Weise haben die Zahlen rechts vom Dezimalpunkt die Gewichte 16-1, 16-2 und so weiter. Um zum Beipiel die Dezimalzahl 512 in Hexadezimalzahlen darzustellen:
Dezimalwert = 512
512 = 2x162 + 0x161 + 0x160 = 200
Hexadezimalwert = 200
Kennzeichnung von hexadezimalen Zahlen
Hexadezimalen Zahlen werden in der Regel Kennzeichen vorangestellt oder angehängt, um Verwechslungen beim Lesen oder Schreiben zu vermeiden und die Unterscheidung zwischen Hexadezimal- und Dezimalzahlen zu erleichtern. Zu den gebräuchlichsten Hexadezimal-Kennzeichen gehören:
| Kennzeichen | Verwendung | Beispiel |
| % | Wird häufig in URLs für bestimmte Zeichen wie Leerzeichen verwendet. | %20 |
| # | Wird in der HTML-Sprache als Farbreferenz verwendet. | #RR5687 |
| 0h | Verwendet in programmierbaren Grafikcoderechnern. | 0h7D |
| \x | Wird in HTML, XML und anderen Sprachen verwendet, um Steuercodes für Zeichen auszudrücken. | \x08: Backspace \x1B: Escape |
| 0x | Wird in der Unix und C-basierter Programmierung verwendet. | 0x54EF |
Es sind auch andere Kennungen gebräuchlich, die jedoch in der Regel auf bestimmte Programmiersprachen beschränkt sind und nicht austauschbar mit anderen Sprachen verwendet werden können.
Programmierer können auf Online-Tools zur Umwandlung von Hexadezimal- in Dezimalzahlen zugreifen, zum Beispiel auf BinaryHexConverter, das die Arbeit mit Hexadezimalzahlen erleichtert.
Vor- und Nachteile von Hexadezimalzahlen
Vorteile
Hexadezimalzahlen sind kompakt und benötigen weniger Speicherplatz, sodass mehr Zahlen in Computersystemen gespeichert werden können. Ein Beispiel dafür ist IPv6, dass hexadezimale Zahlen für die IP-Adressen verwendet. Die geringe Größe von hexadezimalen Zahlen erleichtert auch die Eingabe/Ausgabe im Vergleich zu anderen Zahlensystemen. Da Hexadezimalzahlen leicht in das binäre Zahlensystem umgewandelt werden können und umgekehrt, wird das System häufig in der Computerprogrammierung verwendet. Es ist auch nützlich, um Computerspeicheradressen darzustellen. Eine 32-Bit-Binärzahl wie 11011010110110101101101011011010 wird in Hex kompakt als D6D6D6D6 dargestellt.
Nachteile
Ein Nachteil des Hexadezimalsystems besteht darin, dass es schwierig sein kann, komplexe mathematische Operationen wie Multiplikation und Division durchzuführen. Hexadezimalzahlen sind im Vergleich zu Dezimalzahlen auch schwer zu lesen und zu schreiben.









